لگاریتم ها دارای قوانینی هستند که در این بخش به چند قانون آن اشاره می کنیم.
قانون اول: حاصل جمع لگاریتم a در مبنای c با لگاریتم b در مبنای c برابر است با لگاریتم aضربدر b در مبنای c که به صورت زیر نمایش داده می شود.
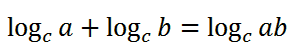
مثال:
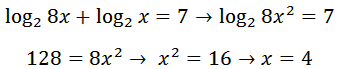
قانون دوم: حاصل تفریق لگاریتم a در مبنای c از لگاریتم b در مبنای c برابر است با لگاریتم a تقسیم بر b در مبنای c که به صورت زیر نمایش داده می شود.
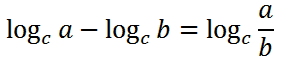
مثال:
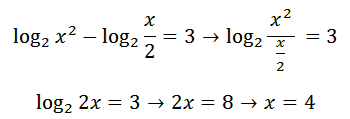
قانون سوم: حاصل لگاریتم a به توان m در مبنای b به توان n برابر m تقسیم n ضربدر لگاریتم a در مبنای b که به صورت زیر نمایش داده می شود.
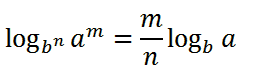
مثال:
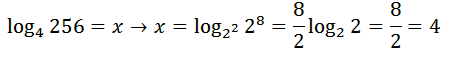
موضوعات مرتبط: رياضي ، ،
برچسبها:
اگر مجموع تعدادي عدد فرد متوالي را داشته باشيم، عدد وسطي برابر است با حاصل تقسيم مجموع عدد ها بر تعدادشان.
سوال) مجموع سه عدد فرد متوالي عدد 153
است . عدد بزرگتر چند است؟
۴۹و۵۱و۵۳
اگر مجموع دو عدد اول ،عددي فرد باشد ،يكي از آن دو عدد اول حتما 2 است
سوال) مجموع دو عدد اول 31 مي باشد .اختلاف آن دو عدد چند است؟
۲۹=۲-۳۱
۲۷=۲-۲۹
بنا براین آن دو عدد ۲و۲۹ است. و اختلاف آندو عدد ۲۷ می باشد.
موضوعات مرتبط: رياضي ، ،
برچسبها:
1 ) جستجو برای الگو: همواره کار حل مساله را با نوعی ادراک شهودی از مساله شروع می کنیم و با بررسی چند حالت خاص به سوی الگوسازی برای حل کامل آن جلو می رویم.
۲) رسم شکل: در هر مساله ای که امکانپذیر باشد رسم یک شکل (اعم از هندسی یا یک نمودار و غیره) می تواند در یافتن حل مساله الهام بخش باشد و رابطه بین اجزا مساله را بهتر نمایان می سازد.
۳) صورتبندی مساله معادل: در بخش قبل دیدیم که گام نخست در حل مساله عبارت است از جمع آوری داده - جستجو - فهمیدن مساله - برقراری ارتباط بین اجزا - حدس زدن و تجزیه تحلیل. ولی اگر همه این کارها به روش معقولی میسر نباشد چه کنیم؟ یعنی اینکه ممکن است کارهای محاسباتی خیلی پیچیده باشد و یا به سادگی نتوانیم حالتهای خاصی را مطرح کنیم تا به بینش لازم برسیم.آنچه در چنین شرایطی توصیه می شود این است که مساله را با مساله ای معادل ولی ساده تر جایگزین کنیم. راه کلی در این گونه معادل سازی به بینش و تجربه های عمومی باز می گردد ولی کارهایی از قبیل دستکاریهای جبری یا مثلثاتی و تفسیر مجدد مساله با زبانی دیگر می تواند موثر باشد.
۴) تغییر مساله: در بعضی مسائل می توانیم مساله مورد نظر را به مساله دیگری تبدیل کنیم. این دو مساله لزوما معادل یکدیگر نیستند ولی حل مساله دوم حل مساله اول را نتیجه می دهد.
۵) انتخاب نمادهای مناسب: از نخستین گامها در حل مساله های ریاضی تبدیل مساله به صورتی نمادین می باشد. در انتخاب نمادها باید هر ایده کلی را ملحوظ داشته و آن را با نمادی بیان کنیم. بی دقتی در انتخاب نمادها ممکن است به از بین رفتن یا مبهم شدن بعضی از روابط منجر شود.
۶) استفاده از تقارن: وجود تقارن در یک مساله موجب می شود که با عملیات کمتری مساله را به جواب برسانیم.
۷) تجزیه به حالتهای ساده تر: گاهی اوقات می توان یک مساله را به تعدادی مساله ساده تر و کوچکتر تبدیل کرد که هر کدام از این مسائل ساده تر را می توان جداگانه در نظر گرفت.
۸) کار عقب رونده: کار عقب رونده یعنی اینکه نتیجه مورد نظر را مفروض گرفته شروع به استنتاج هایی از آن کنیم تا به یک مساله حل شده برسیم. در این صورت گامهای معکوسی را در نظر بگیریم تا به نتیجه مطلوب دست پیدا کنیم.
۹) بررسی نقیض: استفاده از تناقض یعنی مفروض گرفتن نادرستی حکم و با استنتاج به نتیجه نادرست یا متناقضی رسیدن از روشهای آشنا در ریاضیات است.
۱۰) زوجیت: ایده ساده زوج و فرد بودن یکی از ابزارهای بسیار قوی در حل مساله است که کاربردهای وسیعی دارد.
۱۱) بررسی حالتهای حدی: در برخورد اولیه با مساله بعضی اوقات تغییردادن پارامترها بین حدهای پایین و بالای ممکن آنها ایده هایی برای حل مساله به همراه خواهد داشت.
۱۲) تعمیم: معمولا ساده سازی یک مساله راهگشای حل آن است. اما در بعضی موارد حالت تعمیم یافته مساله سهل تر قابل حل است و حالت مورد نظر را می توان به عنوان یک حالت خاص نتیجه گرفت. در واقع ایده تعمیم و در کنار آن مجرد سازی ویژگی خاص ریاضیات نوین است. در پایان اشاره می کنم که سعی کنید یک مساله را در صورت امکان به چند روش حل کنید. این کار باعث بهبود سرعت و خلاقیت شما در حل مسائل دیگر می شود. روشهای مختلف حل مساله بخشهایی از زوایای پنهان مساله را برای شما آشکار می کند
mathroom.ir
موضوعات مرتبط: رياضي ، ،
برچسبها:
مثال: میانگین عددهای 5 و 7 و 1 و 4 و 3 برابر 4 می باشد و میانگین عدد های 15 و 17 و 11 و 14 و 13 برابر 14 است.
![]()
2) اگر همه ی داده ها در عدد ثابتی ضرب شوند میانگین در همان عدد ضرب می شود .
مثال: میانگین عدد های 5 و 7 و 1 و 4 و 3 برابر 4 می باشد و میانگین عدد های 25 و 35 و 5 و20 و 15 برابر 20 است.
![]()
موضوعات مرتبط: رياضي ، ،
برچسبها:
صورت دو نقطه روی خط در نظر می گیریم به شرط آن که این دو نقطه را بتوانیم تعیین مختصات
نماییم سپس رابطه ی بین طول وعرض این نقاط را تشخیص می دهیم.
معادله ای که از مبداً مختصات می گذرد در حالت کلی به چه صورت است ؟ y=ax
چه زمانی دو خط با هم برابراند ؟ هرگاه شیب آنها باهم برابر باشد دو خط باهم موازی هستند.
برای نوشتن معادله ی دو نقطه ی داده شده که طول آنها با هم برابر است چه می کنید؟ معادله ی
خط به صورت x = عدد طول
واگر عرضها باهم برابر باشند معادله ی خط به صورت y =عددعرض است.
موضوعات مرتبط: رياضي ، ،
برچسبها:
تفريق و جمع 4 تقسيم و ضرب3 جذر و توان2 پرانتز1
هر عددي را كه به صو رت كسر بتوان نمايش داد ( صورت و مخرج عضو اعداد صحيح ) عدد گويا است و اعداد گويا را با Q نمايش مي دهيم.
![]() اعداد اعشاري با ريشه كسري جزء اعداد گويا مي باشند كه عبارت اند از :
اعداد اعشاري با ريشه كسري جزء اعداد گويا مي باشند كه عبارت اند از :
a) اعشاري مختوم مانند :1/36
b) اعشاري متناوب ساده مانند : 2/33333و 1/36363636
c) اعشاري متناوب مركب مانند: ....1/3555555
![]() اعداد اعشاري با ريشه راديكالي كه عضو اعداد گويا نمي باشند. مانند : 1/2546983155
اعداد اعشاري با ريشه راديكالي كه عضو اعداد گويا نمي باشند. مانند : 1/2546983155
برچسبها:
موضوعات مرتبط: زيست شناسي ، ،
برچسبها:
پنج اصل متعارفی ، یا مفهوم عمومی اقلیدس
١_چیزهایی که با یک چیز مساوی اند ، با یکدیگر نیز مساوی اند
٢_اگر چیزهای مساوی به چیزهای مساوی اضافه شوند کلها مساوی اند
٣_اگر چیزهای مساوی از چیزهای مساوی کم شوند ، باقیمانده ها مساوی اند
۴_چیزهایی که بر یکدیگر منطبق شوند با یکدیگر مساوی اند
۵_کل از جزء بزرگتر است
و پنج اصل موضوع هندسی از اقلیدس
1
از هر نقطه میتوان خط مستقیمی به هر نقطۀ دیگر کشید
2-
هر خط مستقیم متناهی را می توان روی همان خط به طور نامحدود امتداد داد
3-
میتوان دایره ای با هر نقطۀ دلخواه به عنوان مرکز آن و با شعاعی مساوی هر پاره خط رسم شده از مرکز آن ترسیم کرد
4-
همۀ زوایای قائمه با هم مساوی اند
5-
اگر خط مستقیمی دو خط مستقیم را قطع کند به طوری که مجموع زاویای داخلی یک طرف آن کمتر از دو قائمه باشد این دو خط مستقیم اگر به طور نامحدود امتداد داده شوند ، در طرفی که دو زاویه مجموعا از دو قائمه کمترند ، همدیگر را قطع خواهند کرد
برچسبها:
تصور کنید میخواهید ثابت کنید بینهایت زوج عدد اول وجود دارد که تفاضلشان 2 است؛ به جای آن ثابت میکنید بینهایت زوج عدد اول وجود دارد که تفاضلشان کمتر از 70,000,000 است. این بزرگترین کشف ریاضی سالهای اخیر است.تصور کنید قرار است ثابت کنید تعداد نامتناهی زوج عدد اول وجود دارند که تفاضل آنها دو واحد است. به جای آن ثابت میکنید تعداد نامتناهی زوج عدد اول وجود دارد که تفاضل آنها کمتر از 70 میلیون رقم است. آیا فکر میکنید این شکستی مفتضحانه است و بهتر است درباره آن سکوت کنید؟ اگر این طور فکر میکنید چیزی از دنیای شگفتانگیز ریاضیات نمیدانید.
امنترین اعداد جهانزمانی کارل گاوس ریاضیات را ملکه علوم و نظریه اعداد را ملکه ریاضیات نامیده بود. شاید اگر اعداد اول را از محترم ترین ساکنان قلمرو این ملکه بشماریم سخنی به زیاده نگفته باشیم. اعداد اول اعداد مهمی هستند. نه فقط به این دلیل که امروز بخش بزرگی از اطمینانی که ما به رمزنگاری در کارهای روزمره داریم (مانند تراکنشهای بانکی یا خریدهای اینترنتی با کمک کارتهای اعتباری) به خاطر استفاده از این اعداد است، بلکه به دلیل ماهیت و جایگاهی که در بین اعداد طبیعی دارند مهم به شمار میروند. اعداد طبیعی همان اعداد آشنایی هستند که هنگام شمارش به کار میبریم، از یک شروع میشوند و به ترتیب هر بار یکی به آنها افزوده میشود و مجموعه ای مانند ...و3و2و1 میسازند که به طور نامتناهی ادامه مییابد. در این بین بعضی از اعداد وجود دارند (غیر از 1) که فقط میتوان آنها را به خودشان و به 1 تقسیم کرد. مثلا شما عدد 6 را میتوانید به 1، 2، 3 و 6 تقسیم کنید و باقی مانده شما صفر شود؛ اما عددی مانند 3 فقط قابل تقسیم به 3 و 1 است همینطور عددی مانند 11، 17 یا 1- 2195,000× 2,003,663,613. چنین اعداد طبیعی را که تنها قابل تقسیم بر خود و یک هستند، اعداد اول مینامند. شما به راحتی میتوانید چندین عدد اول را بشمارید، 2،3،5،7،11،13،17،19،23و ... اما هرچقدر اعداد طبیعی بزرگتر میشوند فراوانی و یا چگالی (تعداد اعداد اول در یک فاصله مشخص) نیز کاهش مییابد. هنوز فرمولی پیدا نشده که بتواند اعداد اول را تولید کند و هنوز دقیق نمیدانیم که توزیع این اعداد در بین اعداد طبیعی چگونه است. آیا با اضافه شدن به اعداد طبیعی ممکن است به جایی برسیم که فاصله میان دو عدد اول متوالی نیز به سمت بی نهایت میل کند و به جایی برسیم که هیچ دو عدد اول نزدیک به همی را نتوانیم پیدا کنیم؟
یک فرض قدیمییک فرض قدیمی باعث میشود ریاضیدانها خوشبین باشند که چنین اتفاقی نمیافتد. این فرض که قدمت آن به دوران اقلیدس (سده سوم پیش از میلاد) میرسد، بیان میکند که تعداد نامتناهی زوج عدد اول (دو عدد اول) وجود دارند که فاصله آنها تنها دو واحد است. مثلا 3 و 5 را در نظر بگیرید این دو عدد هر دو اول هستند و تنها دو واحد با هم فاصله دارند. 11 و 13 نیز همین ویژگی را دارند همینطور 17 و 19 و همینطور دو رقم 1- 2195,000× 2,003,663,613 و 1+ 2195,000× 2,003,663,613. حال سوال اینجاست که آیا چنین زوج اعدادی را میتوان وقتی اعضای رشته اعداد طبیعی به اندازه کافی بزرگ باشند هم پیدا کرد؟ اگر این طور باشد باید تعداد نامتناهی از این زوج اعداد وجود داشته باشد.
یک جهش بزرگ |
||
موضوعات مرتبط: رياضي ، ،
برچسبها:



 آمار
وب سایت:
آمار
وب سایت:











